Як використовувати топологічну оптимізацію при моделюванні в області акустики

1. Цільові функції для топологічної оптимізації
2. Приклад статичної задачі механіки конструкцій
3. Проведення топологічної оптимізації в акустичних задачах за допомогою COMSOL Multiphysics®
4. Приклад: одна цільова функція, одна частота
5. Приклад: дві цільові функції, дві частоти
6. Приклад: одна цільова функція, кілька частот
7. Можливості топологічної оптимізації для задач акустики
8. література

Сьогодні Рене Крістенсен (René Christensen) з компанії GN Hearing розповість нам про важливість топологічної оптимізації для задач акустики і продемонструє її використання за допомогою COMSOL Multiphysics.

Топологічна оптимізація - потужний інструмент для пошуку оптимальних рішень інженерних проблем. У цій статті ми детально вивчимо оптимізацію топології стосовно акустиці і відповімо на питання, як знайти оптимальний розподіл акустичного середовища для отримання бажаної характеристики або відгуку. Можливості цього методу оптимізації будуть продемонстровані на кількох прикладах.

Цільові функції для топологічної оптимізації

Багато інженерні завдання включають оптимізацію наявної конструкції або проектування нової конструкції для конкретної прикладної задачі. При цьому величезну важливість має багаторічний досвід роботи в конкретній галузі промисловості і знання практичних прийомів. Однак завдання оптимізації часто бувають настільки складними, що не завжди можна зрозуміти, чи ведуть поетапні зміни конструкції до поліпшення. У таких випадках вдаються до оптимізації в математичному сенсі.

Перш ніж йти далі, давайте згадаємо деякі важливі терміни. У будь-якому завданні оптимізації - параметрів , форми або, в нашому випадку, топології - завжди є щонайменше одна цільова функція. Як правило, нам потрібно мінімізувати цю функцію. У завданнях акустики ми можемо мінімізувати тиск звуку в заданій області, а в задачах механіки конструкцій - напруги в заданій частині конструкції. Ми формулюємо це завдання як

\ Min _ {\ chi} F (\ chi)

де F - цільова функція. В ході оптимізації змінна проектування \ chi змінюється так, щоб отримати оптимальне рішення. Мінлива проектування задана на галузі проектування, яку позначають Ωd і яка зазвичай займає тільки частину кінцево-елементного простору Ω, як показано на малюнку нижче.

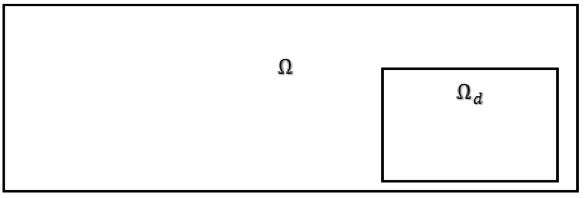
Область проектування зазвичай є підмножиною всієї області кінцевих елементів.

Оскільки змінна проектування являє собою функцію координат в дискретної області кінцевих елементів, що використовується при проектуванні, вона фактично є вектором. У нашому випадку, для простоти, ми будемо говорити про неї як про змінну.

Якщо задачі оптимізації є кілька цільових функцій, то інженер самостійно повинен вирішити, з якими ваговими коефіцієнтами враховуються ці цільові функції. Оскільки в ході оптимізації різні цілі можуть перешкоджати один одному, необхідно звернути особливу увагу на постановку задачі.

Крім цільової функції (функцій) зазвичай в задачі оптимізації є деякі обмеження. Вони характеризують граничні значення габаритів і (або) маси, які застосовуються для даної задачі. В інтерфейсі Optimization (Оптимізація) програмного пакета COMSOL Multiphysics можна систематичним чином задавати змінні проектування, одну або кілька цільових функцій і обмеження.

Приклад статичної задачі механіки конструкцій

В процесі топологічної оптимізації на кожній ітерації змінюються значення змінної проектування, заданої на галузі проектування. Мінлива проектування неперервна в усій області і приймає значення від 0 до 1:

0 <\ chi \ leq 1 \ forall (x, y) \ in \ Omega_d

Ми б хотіли домогтися того, щоб значення змінної проектування виявилися близькі до 0 або 1. Тоді ми отримаємо близьку до дискретної конструкцію, область проектування якої буде охоплена двома дискретними (бінарними) станами. Що це за стану, залежить від фізичного сенсу нашої задачі оптимізації. Оскільки в літературі топологічна оптимізація широко застосовується в задачах механіки конструкцій, ми спочатку вивчимо її стосовно до даної галузі фізики, а в наступному розділі розглянемо її аналог з акустики.

Ми вже обговорювали оптимізацію топології для задач механіки конструкцій за допомогою COMSOL Multiphysics в блозі COMSOL. Коротко викладемо зміст тієї статті. У ній вивчалася так звана MBB-балка (Messerschmitt-Bölkow-Blohm) з метою максимізувати жорсткість, мінімізуючи повну енергію деформації при заданому навантаженні і заданих граничних умовах. Область проектування займала всю область кінцевих елементів. До повної масі конструкції застосовувалося обмеження. В області проектування модуль Юнга задавався змінної проектування \ chi як

E (\ chi) = \ left \ {\ begin {array} {ll} E_0 \ \ textrm {for} \ \ chi = 1 \\ \ textrm {for} \ \ chi = 0 \ end {array} \ right. .

Щоб перейти до бінарним значенням змінної проектування, ми використовували так звану інтерполяцію твердого ізотропного матеріалу з штрафом (SINP),

E (\ chi) = \ chi ^ p E_0,

де p - множник штрафу, зазвичай приймає значення від 3 до 5. Використовуючи цю інтерполяцію і неявну лінійну інтерполяцію щільності матеріалу, вирішувач уникав проміжних значень \ chi, так як вони давали менш вигідні співвідношення жорсткості і ваги. На малюнку нижче показана отримана топологія MBB-балки, отримана в попередній статті.

Оптимізована топологія MBB-балки.

На цьому малюнку чорним відзначений матеріал із заданим користувачем модулем Юнга E0. Білий колір відповідає нульовий жорсткості, вказуючи на області, що залишаються порожніми.

Проведення топологічної оптимізації в акустичних задачах за допомогою COMSOL Multiphysics®

Тепер розглянемо топологічну оптимізацію в акустиці. У завданнях акустики ми стикаємося з залежними від частоти рішеннями, які описують поширення хвиль в акустичних середовищах. Мінлива проектування тепер пов'язана з фізикою звукових хвиль. Замість бінарного розподілу «порожнеча - матеріал» ми хочемо отримати бінарне розподіл «повітря - тверде тіло», де під "твердим тілом" мається на увазі текуче середовище з високою щільністю і високим модулем об'ємної деформації.

Ми поставимо чотири параметри, які описують властивості звичайної і «твердої» середовища в стані спокою і при стисненні: Повітрю пріпішем щільність \ rho_1 і модуль об'ємної деформації K1, а «твердої» середовищі - більш високу щільність \ rho_2 і більш високий модуль об'ємної деформації K2 . Змінюючи змінну проектування, ми змінюємо щільність \ rho і модуль об'ємної деформації K в області проектування так само, як ми змінювали модуль Юнга в прикладі, що відноситься до механіки конструкцій. Однак при цьому потрібно інша інтерполяція, щоб значення матеріальних властивостей не зверталися в нуль при нульовому значенні змінної проектування, а брали значення, характерні для повітря і твердого тіла:

\ Rho (\ chi) = \ left \ {\ begin {array} {ll} \ rho_2 \ \ textrm {for} \ \ chi = 1 \\ \ rho_1 \ \ textrm {for} \ \ chi = 0 \ end { array} \ right.

і

K (\ chi) = \ left \ {\ begin {array} {ll} K_2 \ \ textrm {for} \ \ chi = 1 \\ K_1 \ \ textrm {for} \ \ chi = 0 \ end {array} \ right.

Найпростіший варіант - лінійна інтерполяція, що задається двома крайніми значеннями. Це не кращий підхід, оскільки він не передбачає штрафу за проміжні значення \ chi, і оптимальна конструкція може виявитися не бінарної. Отже, така конструкція буде фізично нездійсненна. В літературі також відомі інші схеми інтерполяції. В описуваних в даному блозі випадках буде використовуватися так зване раціональне наближення матеріальних властивостей (RAMP), см. [1] .

Як і в разі оптимізації для механіки конструкцій, ми задаємо область проектування, в якій шукаємо розподіл матеріалу, що відповідає обмеженням. Обмеження на площу або обсяг можна задати через змінні проектування. Наприклад, обмеження на площу в області проектування можна задати у вигляді нерівності

\ Int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq S_r,

де Sr - відношення площі області, якої приписані властивості твердого тіла, до площі всієї області проектування.

Приклад: одна цільова функція, одна частота

Розглянемо приклад глушника (звукопоглинального пристрою). Для простоти обмежимося двомірної областю. Звичайна характеристика глушника - так званий коефіцієнт загасання (зниження шуму) TL, який задається відношенням вхідної потужності до вихідної потужності:

TL = 10 \ log_ {10} \ left (\ frac {W_i} {W_o} \ right).

Коефіцієнт зниження шуму визначається за так званою трехточечной схемою, запропонованою в [2] . Його ми і виберемо в якості цільової функції, прагнучи максимізувати цей коефіцієнт для однієї частоти (в даному випадку 420 Гц):

\ Max _ {\ chi} TL (420 \ text {Hz}).

Визначено дві області проектування: над трубчастої секцією і під нею. Область проектування обмежена наступним чином: не більше 5% площі області має бути заповнено твердим тілом, тобто 95% повинно бути заповнене повітрям:

\ Int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.05.

Початковий стан галузі проектування - повністю заповнена повітрям область, в якій \ chi = 0. На анімації нижче показаний перехід від початкового стану до підсумкової топології.

Анімація, показує перехід від початкового стану до оптимізованої топології глушника.

Оптимізована конструкція глушника має топологію «камери подвійного розширення», див. [3] . Коефіцієнт зниження шуму на цільової частоті виріс приблизно на 14 дБ, як показано на графіку нижче. Однак на частотах, відмінних від цільової, коефіцієнт зниження шуму також змінився, що може виявитися важливим в конкретної прикладної задачі. Тому оптимізації на одній частоті, як правило, може виявитися недостатньо.

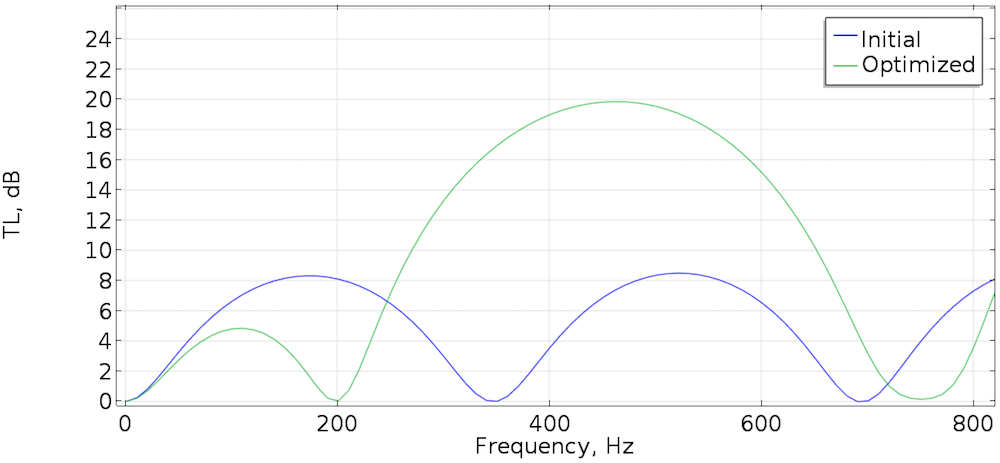
Коефіцієнт зниження шуму для початкового стану і оптимізованої конструкції глушника.

Приклад: дві цільові функції, дві частоти

Давайте перейдемо до задачі оптимізації двох цільових функцій для двох різних частот. Знову розглянемо двомірну кімнату з трьома жорсткими стінами і заданим тиском, прикладеним до лівої стіни кімнати. У кімнаті також виділені дві цільові області Ω1 і Ω2 в правому верхньому і правому нижньому кутку кімнати. Дві цілі формулюються наступним чином:

1. Мінімізувати рівень звукового тиску на частоті f1 і
2. Мінімізувати рівень звукового тиску на частоті f2 = 1,5 f1

при заданій круглої області проектування Ωd і обмеження площі займаної "твердим тілом", яка не повинна перевищувати 10%. Початковий стан - \ chi = 0, тобто вся область проектування заповнена повітрям.

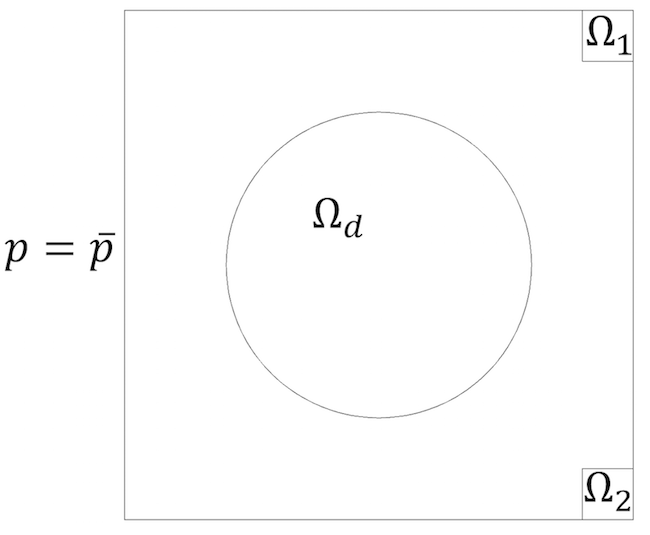
Квадратна двомірна кімната з круглою областю проектування і двома цільовими областями.

Ми повинні вирішити, з якими ваговими коефіцієнтами ми враховуємо дві наші цільові функції або яку важливість ми їм надаємо. У нашому випадку обидві функції однаково важливі, тому завдання формулюється як задача минимакса:

\ Begin {align} \ min _ {\ chi} \ max_ {f_1 f_2} SPL_i (\ chi, f_i) \\ \ text {subject to} \ int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.1 . \ End {align}

На малюнках нижче синім кольором показана оптимізована топологія і тиск звуку на обох частотах в одному масштабі. Зверніть увагу, як оптимізація топології призводить до появи області низького тиску в правому верхньому куті на першій частоті. У той же час ця ж сама топологія забезпечує появу зони низького тиску в правому нижньому кутку на другий частоті. Такого результату було б складно домогтися методом проб і помилок.

Тиск звуку на частоті f1 (зліва) і на частоті f2 (праворуч). Оптимізована топологія показана синім кольором.

Приклад: одна цільова функція, кілька частот

В якості третьої і останній приклад ми оптимізуємо одну цільову функцію для діапазону частот. Джерело звуку випромінює звукові хвилі в двомірну область, в якій спочатку існує циліндричний звукове поле. У задачі присутні дві квадратні області проектування, але ми скористаємося симетрією завдання і змоделюємо лише половину геометрії. У цьому випадку нам потрібно, щоб величина звукового тиску \ overline {p} _ {obj} в точці на відстані 0,4 м перед джерелом звуку по центральній осі симетрії була постійною. Оптимізація виконується в діапазоні частот від 4000 до 4200 Гц (на п'яти частотах з кроком 50 Гц). Для цього ми можемо використовувати функціонал Global Least-Squares Objective (Глобальна цільова функція методу найменших квадратів) в COMSOL Multiphysics з наступною постановкою завдання:

\ Begin {align} \ min _ {\ chi} \ sum_ {i = 1} ^ {5} (\ mid p_i (\ chi, f_i, 0, 0.4) \ mid - \ overline {p} _ {obj}) ^ 2 \\ \ text {subject to} \ int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.1. \ End {align}

Початковий стан як і раніше \ chi = 0. Оптимізована топологія і звукове поле для початкового і оптимізованого стану показані на малюнку нижче.

Тиск звуку в початковому стані (зліва) і оптимізованому стані (праворуч) на частоті 4 кГц. Оптимальна топологія показана синім кольором всередині квадратних областей проектування.

Так як величина тиску звуку в точці спостереження в початковому стані нижче цільового тиску, оптимізація топології веде до появи відбивача, що фокусує звук на центральній осі. Величини тиску звуку до і після оптимізації показані на графіку нижче. Після оптимізації величина тиску виявилася близька до необхідного цільового значення у всьому діапазоні частот.

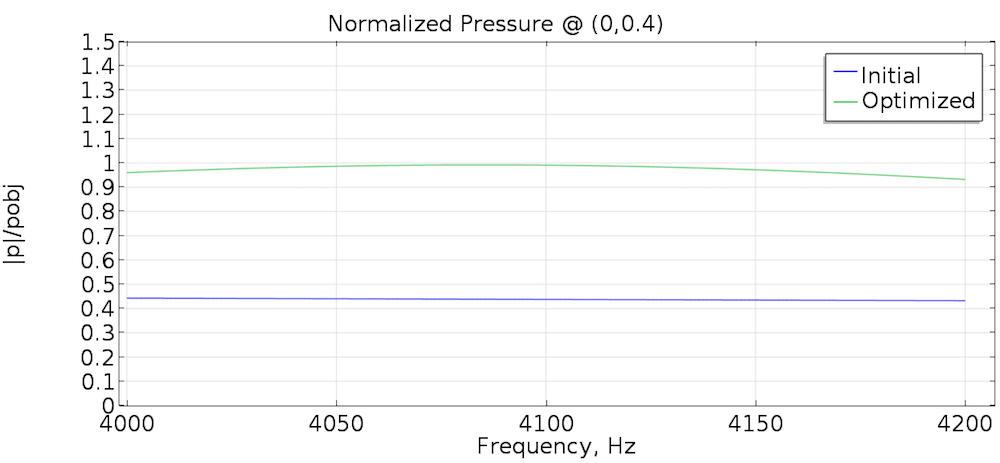
Відношення величини тиску до \ overline {p} _ {obj} для початкової та оптимізованої топології.

Можливості топологічної оптимізації для задач акустики

Топологічна оптимізація - вельми перспективний метод створення нових конструкцій для інженерів, що займаються прикладної акустикою. Як було показано в цій статті, цей метод можна успішно застосовувати в COMSOL Multiphysics. Коректно визначаючи цільові функції і обмеження, можна вирішувати прикладні завдання за допомогою нових і незвичайних топологій, які складно було б виявити традиційними методами.

Я хотів би особливо подякувати доцента Датського технічного університету Нільса Оге (Niels Aage) за плідне обговорення методів оптимізації.

Щоб дізнатися більше про оптимізацію топології для задач акустики в COMSOL Multiphysics, ви можете завантажити наступний приклад з Галереї програм: Topology Optimization of Acoustic Modes in a 2D Room (Топологічна оптимізація при поширенні акустичних мод в двомірної кімнаті).

література

1. MP Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer 2003.
2. TW Wu, GC Wan "Muffler Performance studies and using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss", Trans. ASME: J. Vib. Acoust. 118 (1996) 479-484.
3. Z. Tao, AF Seybert, "A review of current techniques for measuring muffler transmission loss ", SAE International, 2003.

Про приглашенном автора

Рене Крістенсен займається завданнями віброакустікі більше десяти років як консультант (компанія iCapture ApS) і як інженер-проектувальник слухових апаратів (компанії Oticon A / S і GN Hearing A / S). Сферою його спеціалізації є моделювання термовязкіх ефектів в мікроакустіке, і його докторська дисертація була присвячена цій темі. Рене працює старшим інженером-акустиком в дослідницькій групі по технологічної акустиці компанії GN Hearing з 2015 року, займаючись проектуванням та оптимізацією конструкцій слухових апаратів.