Jak wykorzystać optymalizację topologiczną podczas modelowania w dziedzinie akustyki

1. Funkcje docelowe dla optymalizacji topologicznej
2. Przykład statycznego problemu mechaniki strukturalnej
3. Optymalizacja topologii dla zadań akustycznych dzięki COMSOL Multiphysics®
4. Przykład: jedna funkcja celu, jedna częstotliwość
5. Przykład: dwie funkcje docelowe, dwie częstotliwości
6. Przykład: jedna funkcja celu, kilka częstotliwości
7. Możliwości optymalizacji topologicznej dla zadań akustycznych
8. Literatura

Dzisiaj René Christensen z GN Hearing opowie nam o znaczeniu optymalizacji topologicznej dla zadań akustycznych i zademonstruje jej zastosowanie z COMSOL Multiphysics.

Optymalizacja topologiczna jest potężnym narzędziem do znajdowania optymalnych rozwiązań problemów inżynierskich. W tym artykule przyjrzymy się szczegółowo optymalizacji topologii zastosowanej w akustyce i odpowiemy na pytanie, jak znaleźć optymalny rozkład środowiska akustycznego w celu uzyskania pożądanej charakterystyki lub odpowiedzi. Możliwości tej metody optymalizacji zostaną przedstawione w kilku przykładach.

Funkcje docelowe dla optymalizacji topologicznej

Wiele zadań inżynierskich obejmuje optymalizację istniejącego projektu lub zaprojektowanie nowego projektu dla konkretnej aplikacji. Jednocześnie duże znaczenie ma wieloletnie doświadczenie w danej branży i znajomość technik praktycznych. Jednak zadania optymalizacyjne są często tak złożone, że nie zawsze jest możliwe zrozumienie, czy stopniowe zmiany projektowe prowadzą do poprawy. W takich przypadkach uciekają się do optymalizacji w sensie matematycznym.

Zanim pójdziemy dalej, przypomnijmy kilka ważnych terminów. W każdym problemie optymalizacji - parametry , formy lub w naszym przypadku topologia - zawsze istnieje co najmniej jedna funkcja celu . Z reguły musimy zminimalizować tę funkcję. W problemach akustycznych możemy zminimalizować ciśnienie akustyczne w danym obszarze, aw problemach mechaniki strukturalnej naprężenia w danej części konstrukcji. Sformułujemy to zadanie jako

min _ {chi} F (chi)

gdzie F jest funkcją celu. Podczas optymalizacji zmienna projektowa chi jest modyfikowana tak, aby uzyskać optymalne rozwiązanie. Zmienna projektowa jest zdefiniowana w domenie projektowej , która jest oznaczona przez Ωd i która zwykle zajmuje tylko część przestrzeni elementów skończonych Ω , jak pokazano na rysunku poniżej.

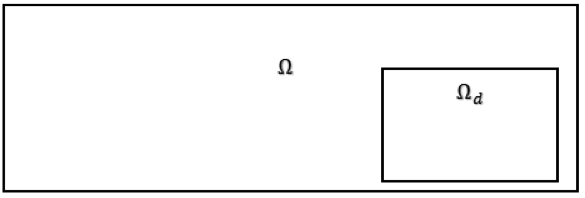
Domena projektowa jest zwykle podzbiorem całej domeny elementów skończonych.

Ponieważ zmienna projektowa jest funkcją współrzędnych w dyskretnym obszarze elementów skończonych wykorzystywanym w projekcie, w rzeczywistości jest to wektor. W naszym przypadku, dla uproszczenia, będziemy mówić o nim jako o zmiennej.

Jeśli problem optymalizacji ma kilka obiektywnych funkcji, inżynier musi samodzielnie zdecydować, z którymi czynnikami ważącymi te obiektywne funkcje są brane pod uwagę. Ponieważ podczas optymalizacji różne cele mogą się wzajemnie zakłócać, należy zwrócić szczególną uwagę na sformułowanie problemu.

Oprócz funkcji celu (ów), zazwyczaj występują pewne ograniczenia w kwestii optymalizacji. Charakteryzują one graniczne wartości wymiarów i (lub) masy mające zastosowanie do danego problemu. W interfejsie optymalizacji pakietu oprogramowania COMSOL Multiphysics można systematycznie ustawiać zmienne projektowe, jedną lub więcej funkcji docelowych i ograniczeń.

Przykład statycznego problemu mechaniki strukturalnej

W procesie optymalizacji topologicznej, przy każdej iteracji, zmieniają się wartości zmiennej projektowej zdefiniowanej w obszarze projektowym. Zmienna projektowa jest ciągła w całym regionie i przyjmuje wartości od 0 do 1:

0 <qq 1 all (x, y) w Omega_d

Chcielibyśmy upewnić się, że wartości zmiennej projektowej są bliskie 0 lub 1. Następnie otrzymujemy projekt zbliżony do dyskretnego, którego obszar projektowy będzie pokryty dwoma dyskretnymi (binarnymi) stanami. Jaki rodzaj zależy od fizycznego znaczenia naszego problemu optymalizacji. Ponieważ w literaturze optymalizacja topologiczna jest szeroko stosowana w problemach mechaniki strukturalnej, najpierw badamy ją w odniesieniu do danej dziedziny fizyki, aw następnej części rozważamy jej analog z akustyki.

Już dyskutowaliśmy Optymalizacja topologii dla mechaniki strukturalnej za pomocą COMSOL Multiphysics na blogu COMSOL. Krótko opisz treść artykułu. Badano tak zwaną wiązkę MBB (Messerschmitt-Bölkow-Blohm), aby zmaksymalizować sztywność, minimalizując całkowitą energię odkształcenia dla danego obciążenia i danych warunków brzegowych. Obszar projektowy zajmował cały obszar elementów skończonych. Zastosowano limit całkowitej masy struktury. W obszarze projektu moduł Younga został zdefiniowany przez zmienną projektową chi as

E (chi) = lewe {begin {array} {ll} E_0 textrm {for} chi = 1 extrm {for} chi = 0 end {array} dobrze. .

Aby przejść do wartości binarnej zmiennej projektowej, zastosowaliśmy tak zwaną interpolację stałego materiału izotropowego z drobnym (SINP),

E (chi) = ^ p E_0,

gdzie p jest mnożnikiem kary, zwykle przyjmującym wartości od 3 do 5. Używając tej interpolacji i niejawnej interpolacji liniowej gęstości materiału, solver unikał pośrednich wartości chi , ponieważ dawały one mniej korzystne współczynniki sztywności i wagi. Poniższy rysunek przedstawia uzyskaną topologię wiązki MBB uzyskaną w poprzednim artykule.

Zoptymalizowana topologia wiązki MBB.

Na tej ilustracji czarny jest oznaczony materiałem ze zdefiniowanym przez użytkownika modułem Eung Young. Biały kolor odpowiada zerowej sztywności, wskazując obszary pozostające puste.

Optymalizacja topologii dla zadań akustycznych dzięki COMSOL Multiphysics®

Rozważ teraz optymalizację topologiczną w akustyce. W problemach akustycznych napotykamy rozwiązania zależne od częstotliwości, które opisują propagację fali w mediach akustycznych. Zmienna projektowa jest teraz powiązana z fizyką fal dźwiękowych. Zamiast binarnej dystrybucji „pustki - materiału”, chcemy uzyskać binarną dystrybucję „powietrza - ciała stałego” , gdzie przez „ciało stałe” rozumiemy płyn o dużej gęstości i wysokim module odkształcenia masowego.

Ustawimy cztery parametry, które opisują właściwości normalnego i „stałego” medium w spoczynku i pod kompresją: Przypisujemy gęstość powietrza rho_1 i moduł odkształcenia masowego K1 do powietrza, a medium stałe - większą gęstość rho_2 i wyższy moduł odkształcenia masowego K2 . Zmieniając zmienną projektową, zmieniamy gęstość rho i moduł masy K w obszarze projektowym, tak jak zmieniliśmy moduł Younga w przykładzie dotyczącym mechaniki strukturalnej. Wymaga to jednak innej interpolacji, aby wartości właściwości materiału nie znikały przy zerowej wartości zmiennej projektowej, ale przyjmowały wartości charakterystyczne dla powietrza i ciała stałego:

rho (chi) = lewe {begin {array} {ll} rho_2 textrm {for} chi = 1 rho_1 textrm {for} chi = 0 end { array}

i

K (chi) = lewe {begin {array} {ll} K_2 textrm {for} chi = 1 K_1 textrm {for} chi = 0 end {array} racja.

Najprostszą opcją jest interpolacja liniowa, podana przez dwie skrajne wartości. Nie jest to najlepsze podejście, ponieważ nie przewiduje kary za pośrednie wartości chi, a optymalna konstrukcja może nie być binarna. Dlatego taka konstrukcja byłaby fizycznie niewykonalna. Inne schematy interpolacji są również znane w literaturze. W przypadkach opisanych na tym blogu zostanie zastosowane tak zwane racjonalne przybliżenie właściwości materiału (RAMP), patrz [1] .

Podobnie jak w przypadku optymalizacji dla mechaniki strukturalnej, wyznaczamy obszar projektowania, w którym poszukujemy dystrybucji materiału spełniającego ograniczenia. Ograniczenia dotyczące obszaru lub objętości można ustawić za pomocą zmiennych projektowych. Na przykład ograniczenie obszaru w obszarze projektu można zdefiniować jako nierówność

int ^ {} _ {Omega_d} chi d Omega_d q S_r,

gdzie Sr jest stosunkiem powierzchni obszaru, do którego właściwości bryły są przypisane obszarowi całego obszaru projektu.

Przykład: jedna funkcja celu, jedna częstotliwość

Rozważmy przykład tłumika (urządzenia pochłaniającego dźwięk). Dla uproszczenia ograniczamy się do obszaru dwuwymiarowego. Zwykłą cechą tłumika jest tak zwany współczynnik tłumienia (redukcja szumów) TL , który jest określony przez stosunek mocy wejściowej do mocy wyjściowej:

TL = 10 log_ {10} z lewej (frak {W_i} {W_o} z prawej).

Współczynnik redukcji hałasu oblicza się za pomocą tak zwanego trzypunktowego schematu zaproponowanego w [2] . Wybierzemy ją jako funkcję celu, próbując zmaksymalizować ten współczynnik dla jednej częstotliwości (w tym przypadku 420 Hz):

max _ {chi} TL (420 tekst {Hz}).

Zidentyfikowano dwa obszary projektowe: powyżej i poniżej odcinka rurowego. Obszar projektowy jest ograniczony w następujący sposób: nie więcej niż 5% powierzchni powinno być wypełnione ciałem stałym, to znaczy 95% powinno być wypełnione powietrzem:

int ^ {} _ {Omega_d} chi d Omega_d 0.05.

Stan początkowy obszaru projektowego to obszar całkowicie wypełniony powietrzem, w którym b = 0. Poniższa animacja pokazuje przejście ze stanu początkowego do końcowej topologii.

Animacja pokazująca przejście ze stanu początkowego do zoptymalizowanej topologii tłumika.

Zoptymalizowana konstrukcja tłumika ma topologię „podwójnej komory ekspansyjnej”, patrz [3] . Współczynnik redukcji szumów przy częstotliwości docelowej wzrósł o około 14 dB, jak pokazano na poniższym wykresie. Jednak przy częstotliwościach innych niż cel zmienił się również współczynnik redukcji szumów, co może być ważne w konkretnym zastosowaniu. Dlatego optymalizacja na pojedynczej częstotliwości z reguły może nie wystarczyć.

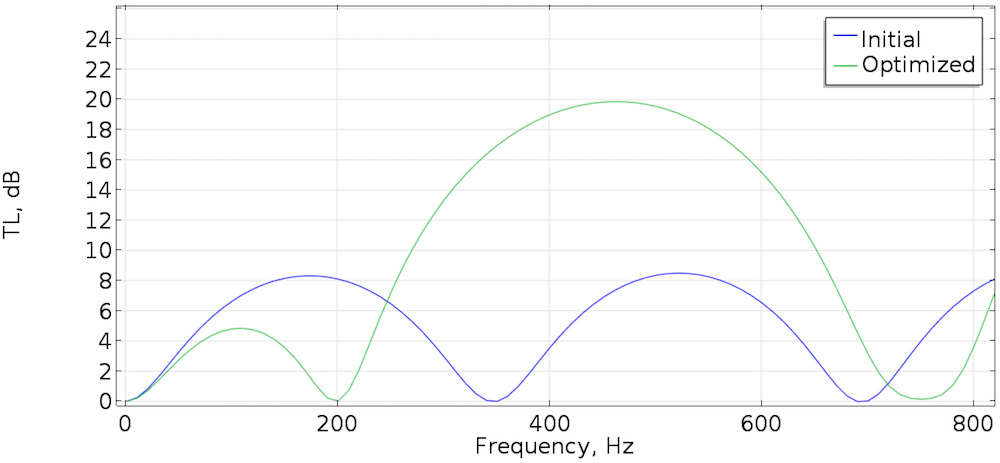
Współczynnik redukcji szumów dla stanu początkowego i zoptymalizowana konstrukcja tłumika.

Przykład: dwie funkcje docelowe, dwie częstotliwości

Przejdźmy do problemu optymalizacji dwóch funkcji celu dla dwóch różnych częstotliwości. Rozważ ponownie dwuwymiarowy pokój z trzema sztywnymi ścianami i określonym naciskiem przyłożonym do lewej ściany pomieszczenia. Pomieszczenie ma również dwa obszary docelowe Ω1 i Ω2 w prawym górnym rogu i prawym dolnym rogu pomieszczenia. Dwa cele są sformułowane w następujący sposób:

1. Zminimalizuj poziom ciśnienia akustycznego przy częstotliwości f1 i
2. Zminimalizuj poziom ciśnienia akustycznego przy częstotliwości f2 = 1,5 f1

dla danego kołowego obszaru Ωd i ograniczenie obszaru zajmowanego przez „ciało stałe”, które nie powinno przekraczać 10%. Stan początkowy to chi = 0, czyli cały obszar projektowy jest wypełniony powietrzem.

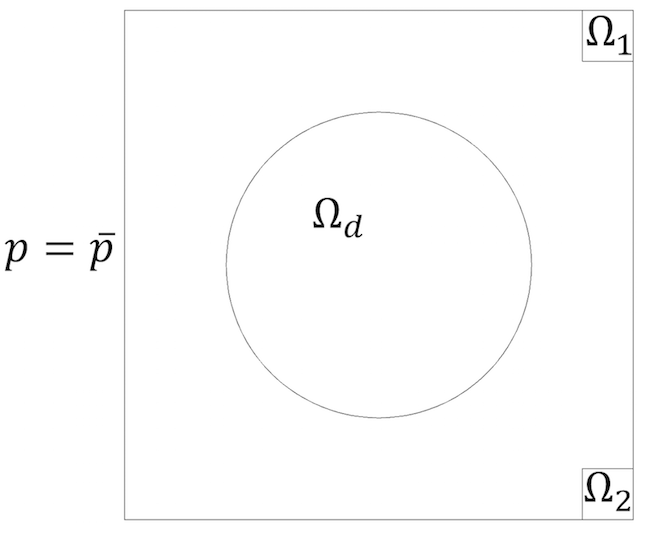
Kwadratowy, dwuwymiarowy pokój o okrągłym obszarze projektu i dwóch obszarach docelowych.

Musimy zdecydować, z jaką wagą uwzględniamy nasze dwie obiektywne funkcje lub jaką wagę im przypisujemy. W naszym przypadku obie funkcje są równie ważne, więc zadanie jest sformułowane jako zadanie minimaksowe :

begin {align} min _ {chi} max_ {f_1 f_2} SPL_i (chi, f_i) text {przedmiot} int ^ {} _ {omega_d} chi d Omega_d q 0.1 . koniec {align}

Na poniższych zdjęciach niebieski pokazuje zoptymalizowaną topologię i ciśnienie dźwięku na obu częstotliwościach w tej samej skali. Zauważ, że optymalizacja topologii prowadzi do pojawienia się obszaru niskiego ciśnienia w prawym górnym rogu pierwszej częstotliwości. Jednocześnie ta sama topologia zapewnia pojawienie się strefy niskiego ciśnienia w prawym dolnym rogu na drugiej częstotliwości. Taki wynik byłby trudny do osiągnięcia metodą prób i błędów.

Ciśnienie akustyczne przy częstotliwości f1 (po lewej) i częstotliwości f2 (po prawej). Zoptymalizowana topologia jest pokazana na niebiesko.

Przykład: jedna funkcja celu, kilka częstotliwości

Jako trzeci i ostatni przykład optymalizujemy jedną funkcję docelową dla zakresu częstotliwości. Źródło dźwięku emituje fale dźwiękowe w dwuwymiarowy obszar, w którym pierwotnie istnieje cylindryczne pole dźwiękowe. W problemie występują dwa kwadratowe obszary projektu, ale używamy symetrii problemu i modelujemy tylko połowę geometrii. W tym przypadku potrzebujemy ciśnienia dźwięku równego {p} _ {obj} w punkcie w odległości 0,4 m przed źródłem dźwięku wzdłuż centralnej osi symetrii, aby była stała. Optymalizacja jest przeprowadzana w zakresie częstotliwości od 4000 do 4200 Hz (przy pięciu częstotliwościach z krokiem 50 Hz). Aby to zrobić, możemy użyć globalnej funkcjonalności obiektywnej najmniejszych kwadratów (globalna funkcja docelowa metody najmniejszych kwadratów) w COMSOL Multiphysics z następującym sformułowaniem problemu:

begin {align} min _ {chi} sum_ {i = 1} ^ {5} (mid p_i (chi, f_i, 0, 0.4) mid - line {p} _ {obj}) ^ 2 text {przedmiot} int ^ {} _ {omega_d} chi d Omega_d q 0.1. koniec {align}

Stan początkowy nadal wynosi chi = 0. Zoptymalizowana topologia i pole dźwiękowe dla stanu początkowego i zoptymalizowanego są pokazane na rysunku poniżej.

Ciśnienie akustyczne w stanie początkowym (po lewej) i stan zoptymalizowany (po prawej) przy 4 kHz. Optymalna topologia jest pokazana na niebiesko wewnątrz kwadratowych obszarów projektowych.

Ponieważ ciśnienie akustyczne w punkcie obserwacyjnym w stanie początkowym jest poniżej ciśnienia docelowego, optymalizacja topologii prowadzi do pojawienia się reflektora skupiającego dźwięk na osi środkowej. Wartości ciśnienia akustycznego przed i po optymalizacji pokazano na poniższym wykresie. Po optymalizacji ciśnienie było zbliżone do pożądanej wartości docelowej w całym zakresie częstotliwości.

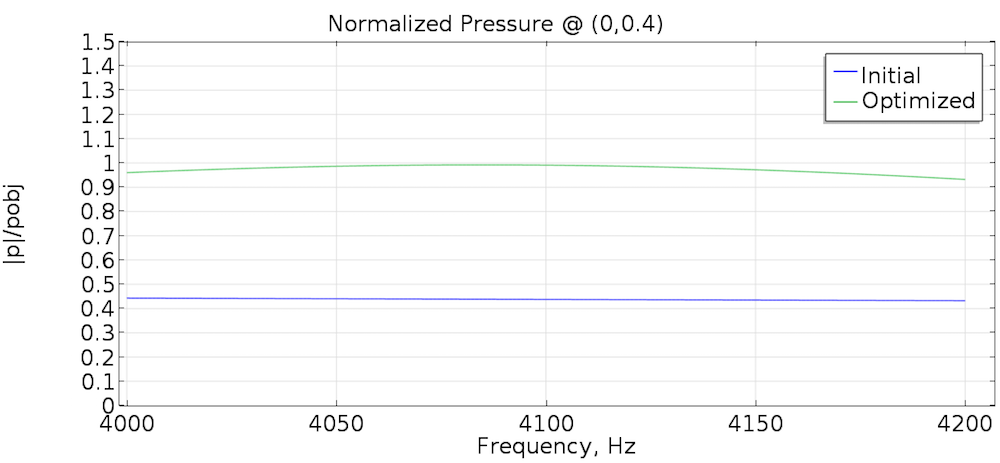
Stosunek ciśnienia do linii {p} _ {obj} dla początkowej i zoptymalizowanej topologii.

Możliwości optymalizacji topologicznej dla zadań akustycznych

Optymalizacja topologiczna jest bardzo obiecującą metodą tworzenia nowych projektów dla inżynierów zajmujących się akustyką stosowaną. Jak pokazano w tym artykule, tę metodę można z powodzeniem zastosować w COMSOL Multiphysics. Poprzez prawidłowe zdefiniowanie funkcji i ograniczeń celu możliwe jest rozwiązanie zastosowanych problemów za pomocą nowych i nietypowych topologii, które byłyby trudne do wykrycia przy użyciu tradycyjnych metod.

Chciałbym szczególnie podziękować profesorowi z Duńskiego Uniwersytetu Technicznego Niels Aage za owocną dyskusję na temat metod optymalizacji.

Aby dowiedzieć się więcej o optymalizacji topologii dla zadań akustycznych w COMSOL Multiphysics, możesz pobrać następujący przykład z Galerii aplikacji: Optymalizacja topologii trybów akustycznych w pomieszczeniu 2D (Optymalizacja topologiczna w propagacji trybów akustycznych w pokoju dwuwymiarowym).

Literatura

1. MP Bendsoe, O. Sigmund, Optymalizacja topologii: teoria, metody i zastosowania , Springer 2003.
2. Mpc Wan, GC Wan „Muffler Performance” ASME: J. Vib. Acoust. 118 (1996) 479-484.
3. Z. Tao, AF Seybert, „Przegląd pomiaru prądu do pomiaru utraty transmisji tłumika”, SAE International , 2003.

O zaproszonym autorze

René Christensen pracuje nad zadaniami wibroakustycznymi od ponad dziesięciu lat jako konsultant (iCapture ApS) oraz jako inżynier projektowania aparatów słuchowych (Oticon A / S i GN Hearing A / S). Jego specjalnością jest modelowanie efektów termo-lepkich w mikroakustyce, a jego rozprawa doktorska była poświęcona temu tematowi. Od 2015 r. Rene pracuje jako starszy inżynier akustyczny w grupie badawczej ds. Akustyki technologicznej w GN Hearing, pracując nad projektowaniem i optymalizacją projektów aparatów słuchowych.