Як выкарыстоўваць тапалагічная аптымізацыю пры мадэляванні ў галіне акустыкі

1. Мэтавыя функцыі для тапалагічнай аптымізацыі
2. Прыклад статычнай задачы механікі канструкцый
3. Правядзенне тапалагічнай аптымізацыі ў акустычных задачах з дапамогай COMSOL Multiphysics®
4. Прыклад: адна мэтавая функцыя, адна частата
5. Прыклад: дзве мэтавыя функцыі, дзве частоты
6. Прыклад: адна мэтавая функцыя, некалькі частот
7. Магчымасці тапалагічнай аптымізацыі для задач акустыкі
8. літаратура

Сёння Рэнэ Крыстэнсэн (René Christensen) з кампаніі GN Hearing раскажа нам пра важнасць тапалагічнай аптымізацыі для задач акустыкі і прадэманструе яе выкарыстанне з дапамогай COMSOL Multiphysics.

Тапалагічная аптымізацыя - магутны інструмент для пошуку аптымальных рашэнняў інжынерных праблем. У гэтым артыкуле мы падрабязна вывучым аптымізацыю тапалогіі дачыненні да акустыцы і адкажам на пытанне, як знайсці аптымальнае размеркаванне акустычнай асяроддзя для атрымання жаданай характарыстыкі або водгуку. Магчымасці гэтага метаду аптымізацыі будуць прадэманстраваны на некалькіх прыкладах.

Мэтавыя функцыі для тапалагічнай аптымізацыі

Шматлікія інжынерныя задачы ўключаюць аптымізацыю наяўнай канструкцыі або праектаванне новай канструкцыі для канкрэтнай прыкладной задачы. Пры гэтым велізарную важнасць мае шматгадовы вопыт працы ў канкрэтнай галіны прамысловасці і веданне практычных прыёмаў. Аднак задачы аптымізацыі часта бываюць настолькі складанымі, што не заўсёды можна зразумець, ці вядуць паэтапныя змены канструкцыі да паляпшэння. У такіх выпадках звяртаюцца да аптымізацыі ў матэматычным сэнсе.

Перш чым ісці далей, давайце ўспомнім некаторыя важныя тэрміны. У любой задачы аптымізацыі - параметраў , формы ці, у нашым выпадку, тапалогіі - заўсёды маецца па меншай меры адна мэтавая функцыя. Як правіла, нам патрабуецца мінімізаваць гэтую функцыю. У задачах акустыкі мы можам мінімізаваць ціск гуку ў зададзенай вобласці, а ў задачах механікі канструкцый - напружання ў зададзенай часткі канструкцыі. Мы фармулюем гэтую задачу як

\ Min _ {\ chi} F (\ chi)

дзе F - мэтавая функцыя. У ходзе аптымізацыі пераменная праектавання \ chi змяняецца так, каб атрымаць аптымальнае рашэнне. Пераменная праектавання зададзена на галіне праектавання, якую абазначаюць Ωd і якая звычайна займае толькі частку вядома-элементнага прасторы Ω, як паказана на малюнку ніжэй.

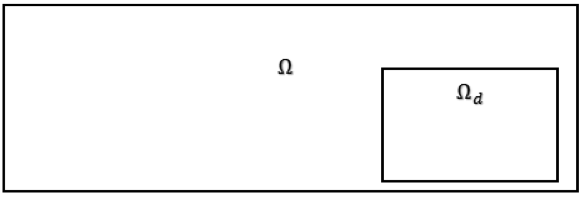
Вобласць праектавання звычайна з'яўляецца падмноствам ўсёй вобласці канчатковых элементаў.

Паколькі пераменная праектавання ўяўляе сабой функцыю каардынат у дыскрэтнай вобласці канчатковых элементаў, што выкарыстоўваецца пры праектаванні, яна фактычна з'яўляецца вектарам. У нашым выпадку, для прастаты, мы будзем казаць пра яе як пра зменнай.

Калі задачы аптымізацыі ёсць некалькі мэтавых функцый, то інжынер самастойна павінен вырашыць, з якімі вагавымі каэфіцыентамі ўлічваюцца гэтыя мэтавыя функцыі. Паколькі ў ходзе аптымізацыі розныя мэты могуць перашкаджаць адзін аднаму, неабходна звярнуць асаблівую ўвагу на пастаноўку задачы.

Акрамя мэтавай функцыі (функцый) звычайна ў задачы аптымізацыі ёсць некаторыя абмежаванні. Яны характарызуюць гранічныя значэнні габарытаў і (або) масы, прыдатныя для разгляданай задачы. У інтэрфейсе Optimization (Аптымізацыя) праграмнага пакета COMSOL Multiphysics можна сістэматычным чынам задаваць зменныя праектавання, адну або некалькі мэтавых функцый і абмежаванні.

Прыклад статычнай задачы механікі канструкцый

У працэсе тапалагічнай аптымізацыі на кожнай ітэрацыі змяняюцца значэння зменнай праектавання, зададзенай на вобласці праектавання. Пераменная праектавання бесперапынная ва ўсёй вобласці і прымае значэнні ад 0 да 1:

0 <\ chi \ leq 1 \ forall (x, y) \ in \ Omega_d

Мы б хацелі дабіцца таго, каб значэння зменнай праектавання апынуліся блізкія да 0 або 1. Тады мы атрымаем блізкую да дыскрэтнай канструкцыю, вобласць праектавання якой будзе ахоплена двума дыскрэтнымі (бінарнымі) станамі. Што гэта за стану, залежыць ад фізічнага сэнсу нашай задачы аптымізацыі. Паколькі ў літаратуры тапалагічная аптымізацыя шырока ўжываецца ў задачах механікі канструкцый, мы спачатку вывучым яе ў дачыненні да дадзенай галіне фізікі, а ў наступным раздзеле разгледзім яе аналаг з акустыкі.

Мы ўжо абмяркоўвалі аптымізацыю тапалогіі для задач механікі канструкцый з дапамогай COMSOL Multiphysics у блогу COMSOL. Коратка выкладзем ўтрыманне таго артыкула. У ёй вывучалася так званая MBB-бэлька (Messerschmitt-Bölkow-Blohm) з мэтай максымізаваць калянасць, мінімізуючы поўную энергію дэфармацыі пры зададзенай нагрузцы і зададзеных межавых умовах. Вобласць праектавання займала ўсю вобласць канчатковых элементаў. Да поўнай масе канструкцыі ўжывалася абмежаванне. У галіне праектавання модуль Юнга задавалася зменнай праектавання \ chi як

E (\ chi) = \ left \ {\ begin {array} {ll} E_0 \ \ textrm {for} \ \ chi = 1 \\ \ textrm {for} \ \ chi = 0 \ end {array} \ right. .

Каб перайсці да бінарнага значэнні зменнай праектавання, мы выкарыстоўвалі так званую інтэрпаляцыю цвёрдага ізатропнай матэрыялу са штрафам (SINP),

E (\ chi) = \ chi ^ p E_0,

дзе p - множнік штрафу, звычайна які прымае значэнні ад 3 да 5. Выкарыстоўваючы гэтую інтэрпаляцыю і няяўную лінейную інтэрпаляцыю шчыльнасці матэрыялу, решатель пазбягаў прамежкавых значэнняў \ chi, так як яны давалі менш выгадныя суадносін калянасці і вагі. На малюнку ніжэй паказана атрыманая тапалогія MBB-бэлькі, атрыманая ў папярэдняй артыкуле.

Аптымізаваная тапалогія MBB-бэлькі.

На гэтым малюнку чорным адзначаны матэрыял з зададзеным карыстальнікам модулем Юнга E0. Белы колер адпавядае нулявы калянасці, паказваючы на ​​вобласці, якія застаюцца пустымі.

Правядзенне тапалагічнай аптымізацыі ў акустычных задачах з дапамогай COMSOL Multiphysics®

Зараз разгледзім тапалагічная аптымізацыю ў акустыцы. У задачах акустыкі мы сутыкаемся за залежнымі ад частоты рашэннямі, якія апісваюць распаўсюджванне хваль у акустычных асяроддзях. Пераменная праектавання цяпер звязана з фізікай гукавых хваль. Замест бінарнага размеркавання «пустата - матэрыял» мы хочам атрымаць бінарнае размеркаванне «паветра - цвёрдае цела", дзе пад "цвёрдым целам" маецца на ўвазе цякучая серада з высокай шчыльнасцю і высокім модулем аб'ёмнай дэфармацыі.

Мы задамо чатыры параметру, якія апісваюць ўласцівасці звычайнай і «цвёрдай» асяроддзя ў стане спакою і пры сціску: Паветра Прыпішы шчыльнасць \ rho_1 і модуль аб'ёмнай дэфармацыі K1, а «цвёрдай» асяроддзі - больш высокую шчыльнасць \ rho_2 і больш высокі модуль аб'ёмнай дэфармацыі K2 . Змяняючы зменную праектавання, мы мяняем шчыльнасць \ rho і модуль аб'ёмнай дэфармацыі K ў галіне праектавання гэтак жа, як мы мянялі модуль Юнга ў прыкладзе, які адносіцца да механікі канструкцый. Аднак пры гэтым патрабуецца іншая інтэрпаляцыя, каб значэння матэрыяльных уласцівасцяў не звярталіся ў нуль пры нулявым значэнні зменнай праектавання, а прымалі значэння, характэрныя для паветра і цвёрдага цела:

\ Rho (\ chi) = \ left \ {\ begin {array} {ll} \ rho_2 \ \ textrm {for} \ \ chi = 1 \\ \ rho_1 \ \ textrm {for} \ \ chi = 0 \ end { array} \ right.

і

K (\ chi) = \ left \ {\ begin {array} {ll} K_2 \ \ textrm {for} \ \ chi = 1 \\ K_1 \ \ textrm {for} \ \ chi = 0 \ end {array} \ right.

Самы просты варыянт - лінейная інтэрпаляцыя, задаваць двума крайнімі значэннямі. Гэта не лепшы падыход, паколькі ён не прадугледжвае штрафу за прамежкавыя значэння \ chi, і аптымальная канструкцыя можа апынуцца не бінарнай. Такім чынам, такая канструкцыя будзе фізічна няздзейсная. У літаратуры таксама вядомыя іншыя схемы інтэрпаляцыі. У апісваных у дадзеным блогу выпадках будзе выкарыстоўвацца так званае рацыянальнае набліжэнне матэрыяльных уласцівасцяў (RAMP), см. [1] .

Як і ў выпадку аптымізацыі для механікі канструкцый, мы задаем вобласць праектавання, у якой шукаем размеркаванне матэрыялу, якое адказвае абмежаванням. Абмежаванні на плошчу або аб'ём можна задаць праз зменныя праектавання. Напрыклад, абмежаванне на плошчу ў галіне праектавання можна задаць у выглядзе няроўнасці

\ Int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq S_r,

дзе Sr - стаўленне плошчы вобласці, якой прыпісаны ўласцівасці цвёрдага цела, да плошчы ўсёй вобласці праектавання.

Прыклад: адна мэтавая функцыя, адна частата

Разгледзім прыклад глушыцеля (Гукапаглынальныя прылады). Для прастаты абмяжуемся двухмернай вобласцю. Звычайная характарыстыка глушыцеля - так званы каэфіцыент згасання (зніжэння шуму) TL, які задаецца стаўленнем ўваходных магутнасці да выхадны магутнасці:

TL = 10 \ log_ {10} \ left (\ frac {W_i} {W_o} \ right).

Каэфіцыент зніжэння шуму вылічаецца па так званай трохкропкавых схеме, прапанаванай у [2] . Яго мы і абярэм у якасці мэтавай функцыі, імкнучыся максымізаваць гэты каэфіцыент для адной частоты (у дадзеным выпадку 420 Гц):

\ Max _ {\ chi} TL (420 \ text {Hz}).

Вызначаны дзве вобласці праектавання: над трубчастай секцыяй і пад ёй. Вобласць праектавання абмежаваная наступным чынам: не больш за 5% плошчы вобласці павінна быць запоўнена цвёрдым целам, то ёсць 95% павінна быць запоўнена паветрам:

\ Int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.05.

Зыходны стан галіне праектавання - цалкам запоўненая паветрам вобласць, у якой \ chi = 0. На анімацыі ніжэй паказаны пераход ад пачатковага стану да выніковай тапалогіі.

Анімацыя, якая паказвае пераход ад пачатковага стану да аптымізаванай тапалогіі глушыцеля.

Аптымізаваная канструкцыя глушыцеля мае тапалогію «камеры падвойнага пашырэння», гл. [3] . Каэфіцыент зніжэння шуму на мэтавай частаце вырас прыкладна на 14 дб, як паказана на графіцы ніжэй. Аднак на частотах, выдатных ад мэтавай, каэфіцыент зніжэння шуму таксама змяніўся, што можа апынуцца важным у канкрэтнай прыкладной задачы. Таму аптымізацыі на адной частаце, як правіла, можа апынуцца недастаткова.

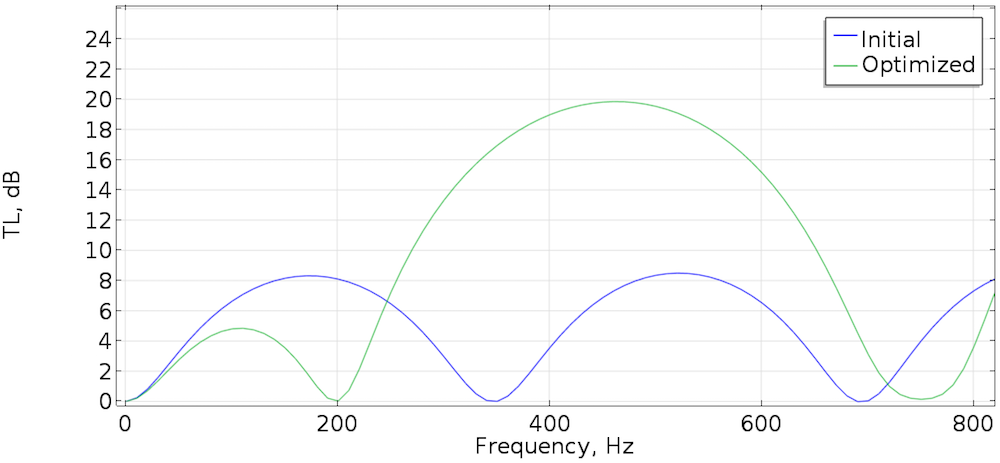
Каэфіцыент зніжэння шуму для пачатковага стану і аптымізаванай канструкцыі глушыцеля.

Прыклад: дзве мэтавыя функцыі, дзве частоты

Давайце пяройдзем да задачы аптымізацыі двух мэтавых функцый для двух розных частот. Зноў разгледзім двухмерную пакой з трыма жорсткімі сценамі і зададзеным ціскам, прыкладзеным да левай сцяне пакоя. У пакоі таксама выдзелены дзве мэтавыя вобласці Ω1 і Ω2 ў правым верхнім і правым ніжнім куце пакоя. Дзве мэты фармулююцца наступным чынам:

1. Мінімізаваць узровень гукавога ціску на частаце f1 і
2. Мінімізаваць узровень гукавога ціску на частаце f2 = 1,5 f1

пры зададзенай круглай галіне праектавання Ωd і абмежаванні плошчы займаемай "цвёрдым целам", якая не павінна перавышаць 10%. Зыходны стан - \ chi = 0, то ёсць уся вобласць праектавання запоўненая паветрам.

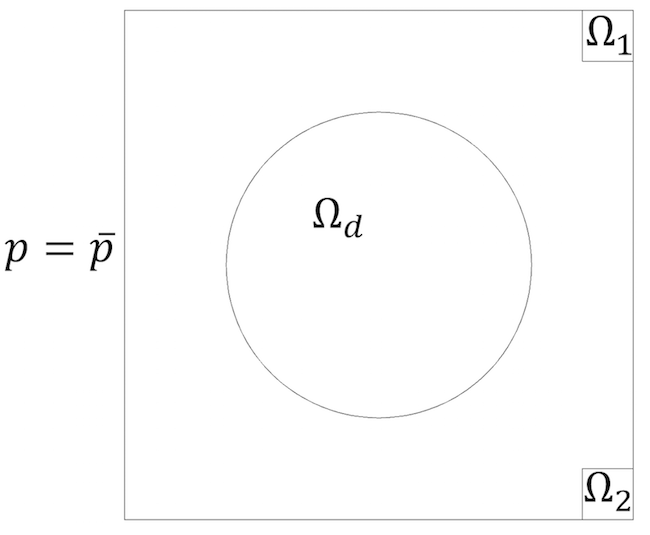
Квадратная двухмерная пакой з круглай вобласцю праектавання і двума мэтавымі абласцямі.

Мы павінны вырашыць, з якімі вагавымі каэфіцыентамі мы ўлічваем дзве нашы мэтавыя функцыі або якую важнасць мы ім надаём. У нашым выпадку абедзве функцыі аднолькава важныя, таму задача фармулюецца як задача минимакса:

\ Begin {align} \ min _ {\ chi} \ max_ {f_1 f_2} SPL_i (\ chi, f_i) \\ \ text {subject to} \ int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.1 . \ End {align}

На малюнках ніжэй сінім колерам паказана аптымізаваная тапалогія і ціск гуку на абедзвюх частотах ў адным маштабе. Звярніце ўвагу, як аптымізацыя тапалогіі прыводзіць да з'яўлення галіне нізкага ціску ў правым верхнім куце на першай частаце. У той жа час гэтая ж самая тапалогія забяспечвае з'яўленне зоны нізкага ціску ў правым ніжнім куце на другі частаце. Такога выніку было б складана дамагчыся метадам спроб і памылак.

Ціск гуку на частаце f1 (злева) і на частаце f2 (справа). Аптымізаваная тапалогія паказана сінім колерам.

Прыклад: адна мэтавая функцыя, некалькі частот

У якасці трэцяга і апошняга прыкладу мы аптымізуем адну мэтавую функцыю для дыяпазону частот. Крыніца гуку выпраменьвае гукавыя хвалі ў двухмерную вобласць, у якой першапачаткова існуе цыліндрычнае гукавое поле. У задачы прысутнічаюць дзве квадратныя галіне праектавання, але мы скарыстаемся сіметрыяй задачы і змадэлюем толькі палову геаметрыі. У гэтым выпадку нам трэба, каб велічыня гукавога ціску \ overline {p} _ {obj} ў кропцы на адлегласці 0,4 м перад крыніцай гуку па цэнтральнай восі сіметрыі была пастаяннай. Аптымізацыя выконваецца ў дыяпазоне частот ад 4000 да 4200 Гц (на пяці частотах з крокам 50 Гц). Для гэтага мы можам выкарыстоўваць функцыянал Global Least-Squares Objective (Глабальная мэтавая функцыя метаду найменшых квадратаў) у COMSOL Multiphysics з наступнага пастаноўкай задачы:

\ Begin {align} \ min _ {\ chi} \ sum_ {i = 1} ^ {5} (\ mid p_i (\ chi, f_i, 0, 0.4) \ mid - \ overline {p} _ {obj}) ^ 2 \\ \ text {subject to} \ int ^ {} _ {\ Omega_d} \ chi d \ Omega_d \ leq 0.1. \ End {align}

Зыходны стан па-ранейшаму \ chi = 0. Аптымізаваная тапалогія і гукавое поле для пачатковай і аптымізаванага стану паказаны на малюнку ніжэй.

Ціск гуку ў пачатковым стане (злева) і аптымізаваным стане (справа) на частаце 4 кГц. Аптымальная тапалогія паказана сінім колерам ўнутры квадратных абласцей праектавання.

Бо велічыня ціску гуку ў кропцы назірання ў пачатковым стане ніжэй мэтавага ціску, аптымізацыя тапалогіі вядзе да з'яўлення адбівальніка, факусуюць гук на цэнтральнай восі. Велічыні ціску гуку да і пасля аптымізацыі паказаны на графіцы ніжэй. Пасля аптымізацыі велічыня ціску апынулася блізкая да патрабаванага мэтавым значэнні ва ўсім дыяпазоне частот.

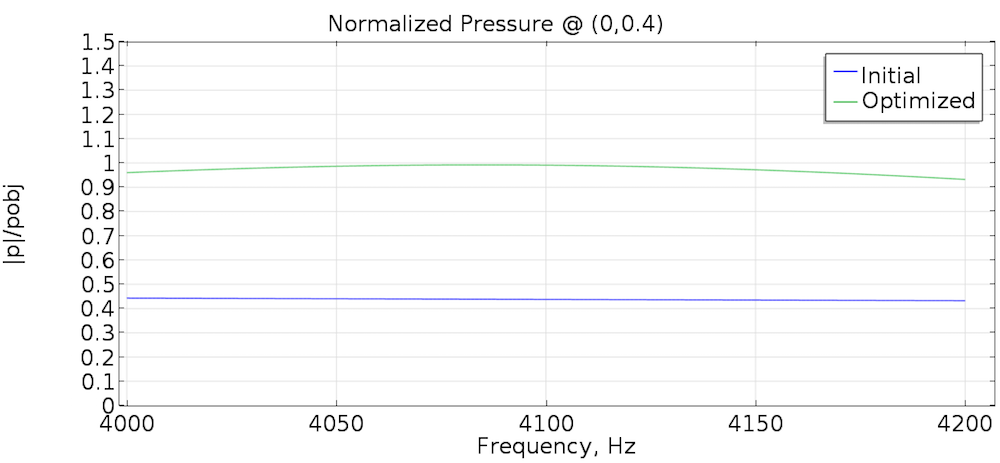
Стаўленне велічыні ціску к \ overline {p} _ {obj} для пачатковай і аптымізаванай тапалогіі.

Магчымасці тапалагічнай аптымізацыі для задач акустыкі

Тапалагічная аптымізацыя - вельмі перспектыўны метад стварэння новых канструкцый для інжынераў, якія займаюцца прыкладной акустыкай. Як было паказана ў гэтым артыкуле, гэты метад можна паспяхова ўжываць у COMSOL Multiphysics. Карэктна вызначаючы мэтавыя функцыі і абмежаванні, можна вырашаць прыкладныя задачы з дапамогай новых і незвычайных тапалогій, якія складана было б выявіць традыцыйнымі метадамі.

Я хацеў бы асабліва падзякаваць дацэнта Дацкага тэхнічнага універсітэта Нільса Огэ (Niels Aage) за плённае абмеркаванне метадаў аптымізацыі.

Каб даведацца больш аб аптымізацыі тапалогіі для задач акустыкі ў COMSOL Multiphysics, вы можаце загрузіць наступны прыклад з Галерэі прыкладанняў: Topology Optimization of Acoustic Modes in a 2D Room (Тапалагічнай аптымізацыя пры распаўсюдзе акустычных мод у двухмернай пакоі).

літаратура

1. MP Bendsoe, O. Sigmund, Topology Optimization: Theory, Methods, and Applications, Springer 2003.
2. TW Wu, GC Wan "Muffler Performance studies and using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss", Trans. ASME: J. Vib. Acoust. 118 (1996 г.) 479-484.
3. Z. Tao, AF Seybert, "A review of current techniques for measuring muffler transmission loss ", SAE International 2003.

Аб запрошаных аўтараў

Рэнэ Крыстэнсэн займаецца задачамі виброакустики больш за дзесяць гадоў як кансультант (кампанія iCapture ApS) і як інжынер-праекціроўшчык слыхавых апаратаў (кампаніі Oticon A / S і GN Hearing A / S). Сферай яго спецыялізацыі з'яўляецца мадэляванне термовязких эфектаў ў микроакустике, і яго доктарская дысертацыя была прысвечана гэтай тэме. Рэнэ працуе старэйшым інжынерам-акустыка ў даследчай групе па тэхналагічнай акустыцы кампаніі GN Hearing з 2015 года, займаючыся праектаваннем і аптымізацыяй канструкцый слыхавых апаратаў.